PhD Dissertation: Bayesian Methods for Mineral Processing Operations
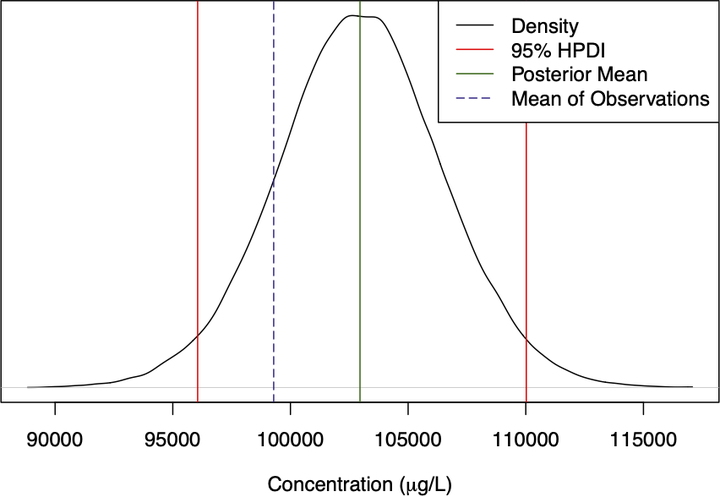 Result of Bayesian Mass Balance
Result of Bayesian Mass Balance
I have finally gotten around to uploading my dissertation for my PhD in Mining Engineering, after submitting the final copy to Virginia Tech in May 2022. After a brief literature review, the dissertation overviews four applications of Bayesian statistical inference to general mineral processing problems. The topics can be broken up as such:
-
Linear Regression
- Ch 3: Bayesian data reconciliation of a process, which allows for uncertainty quantification of estimates and model selection.
- Ch 4: Use of Bayesian inference with an autoregressive model to methodically estimate steady state concentrations.
-
Gaussian Process Regression
- Ch 5: Bayesian optimization of a process simulation with unknown dynamics.
- Ch 6: Active learning acquisition of computer simulator data, for the purposes of improved prediction using the Kennedy and O’Hagan calibration framework. This novel statistical method has been coined KOH-IMSPE.
Chapter 3 was published as The utility of Bayesian data reconciliation for separations in 2021.
Chapter 4 has been resubmitted for publication after some minor edits and is hopefully forthcoming.
Chapter 5 requires some more data to be collected and revision before submission. We hope to add a real data example to the simulator example found within the dissertation text.
I am the most excited about publishing Chapter 6. The novel statistical method developed in this chapter has applications outside of mineral processing. After collection of both real data and data from a simulator, one would want to use the real data to calibrate the simulator (also known as inverse modeling or adjusting tuning parameters). For an expensive to evaluate simulator it would be smart to collect simulation runs near the best estimate of a tuning parameter, in order to reduce simulator computation time.
In the below figure we see KOH-IMSPE doing just that. Let the $u$ axis be entertained values for a simulator tuning parameter, and the $X$ axis be independent variables we can change or observe when collecting real world data (we can’t observe tuning parameters, such the acceleration due to gravity, but we can measure some independent variables, such as an object’s height before falling to the ground). Furthermore, let $u^\star$ be the true value of a tuning parameter and $\hat{u}$ be the best estimate of $u^\star$ given the observed data. It can be seen below that KOH-IMSPE sequentially gathers simulator data near $\hat{u}$, while allowing for some exploration.

Evidence that this acquisition criteria requires less simulator data for the same level of predictive accuracy of other methods is provided in the dissertation dissertation. The details of an application on a real data set are being worked out as an included section before submission.